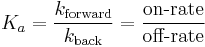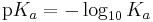Dissociation constant
In chemistry, biochemistry, and pharmacology, a dissociation constant is a specific type of equilibrium constant that measures the propensity of a larger object to separate (dissociate) reversibly into smaller components, as when a complex falls apart into its component molecules, or when a salt splits up into its component ions. The dissociation constant is usually denoted 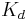 and is the inverse of the association constant. In the special case of salts, the dissociation constant can also be called an ionization constant.
and is the inverse of the association constant. In the special case of salts, the dissociation constant can also be called an ionization constant.
For a general reaction
in which a complex 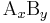 breaks down into x A subunits and y B subunits, the dissociation constant is defined
breaks down into x A subunits and y B subunits, the dissociation constant is defined
where [A], [B], and [AxBy] are the concentrations of A, B, and the complex AxBy, respectively.
One reason for the popularity of the dissociation constant in biochemistry and pharmacology is that in the frequently encountered case where x=y=1, Kd has a simple physical interpretation: when [A]=Kd, [B]=[AB] or equivalently [AB]/([B]+[AB])=1/2. That is, Kd, which has the dimensions of concentration, equals the concentration of free A at which half of the total molecules of B are associated with A. This simple interpretation does not apply for higher values of x or y.
Contents |
Protein-ligand binding
The dissociation constant is commonly used to describe the affinity between a ligand (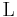 ) (such as a drug) and a protein (
) (such as a drug) and a protein (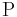 ) i.e. how tightly a ligand binds to a particular protein. Ligand-protein affinities are influenced by non-covalent intermolecular interactions between the two molecules such as hydrogen bonding, electrostatic interactions, hydrophobic and Van der Waals forces. They can also be affected by high concentrations of other macromolecules, which causes macromolecular crowding.[1][2]
) i.e. how tightly a ligand binds to a particular protein. Ligand-protein affinities are influenced by non-covalent intermolecular interactions between the two molecules such as hydrogen bonding, electrostatic interactions, hydrophobic and Van der Waals forces. They can also be affected by high concentrations of other macromolecules, which causes macromolecular crowding.[1][2]
The formation of a ligand-protein complex (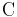 ) can be described by a two-state process
) can be described by a two-state process
the corresponding dissociation constant is defined
where [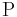 ], [
], [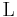 ] and [
] and [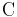 ] represent molar concentrations of the protein, ligand and complex, respectively.
] represent molar concentrations of the protein, ligand and complex, respectively.
The dissociation constant has molar units (M), which correspond to the concentration of ligand [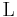 ] at which the binding site on a particular protein is half occupied, i.e. the concentration of ligand, at which the concentration of protein with ligand bound [
] at which the binding site on a particular protein is half occupied, i.e. the concentration of ligand, at which the concentration of protein with ligand bound [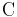 ], equals the concentration of protein with no ligand bound [
], equals the concentration of protein with no ligand bound [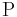 ]. The smaller the dissociation constant, the more tightly bound the ligand is, or the higher the affinity between ligand and protein. For example, a ligand with a nanomolar (nM) dissociation constant binds more tightly to a particular protein than a ligand with a micromolar (
]. The smaller the dissociation constant, the more tightly bound the ligand is, or the higher the affinity between ligand and protein. For example, a ligand with a nanomolar (nM) dissociation constant binds more tightly to a particular protein than a ligand with a micromolar ( M) dissociation constant.
M) dissociation constant.
Sub-picomolar dissociation constants as a result of non-covalent binding interactions between two molecules are rare. Nevertheless, there are some important exceptions. Biotin and avidin bind with a dissociation constant of roughly 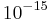 M = 1 fM = 0.000001 nM.[3] Ribonuclease inhibitor proteins may also bind to ribonuclease with a similar
M = 1 fM = 0.000001 nM.[3] Ribonuclease inhibitor proteins may also bind to ribonuclease with a similar 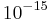 M affinity.[4] The dissociation constant for a particular ligand-protein interaction can change significantly with solution conditions (e.g. temperature, pH and salt concentration). The effect of different solution conditions is to effectively modify the strength of any intermolecular interactions holding a particular ligand-protein complex together.
M affinity.[4] The dissociation constant for a particular ligand-protein interaction can change significantly with solution conditions (e.g. temperature, pH and salt concentration). The effect of different solution conditions is to effectively modify the strength of any intermolecular interactions holding a particular ligand-protein complex together.
Drugs can produce harmful side effects through interactions with proteins for which they were not meant to or designed to interact. Therefore much pharmaceutical research is aimed at designing drugs that bind to only their target proteins (Negative Design) with high affinity (typically 0.1-10 nM) or at improving the affinity between a particular drug and its in-vivo protein target (Positive Design).
Antibodies
In the specific case of antibodies (Ab) binding to antigen (Ag), usually the affinity constant is used. It is the inverted dissociation constant.
This chemical equilibrium is also the ratio of the on-rate (kforward) and off-rate (kback) constants. Two antibodies can have the same affinity, but one may have both a high on- and off-rate constant, while the other may have both a low on- and off-rate constant.
Acid base reactions
For the deprotonation of acids, K is known as Ka, the acid dissociation constant. Stronger acids, for example sulfuric or phosphoric acid, have larger dissociation constants; weaker acids, like acetic acid, have smaller dissociation constants.
(The symbol 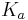 , used for the acid dissociation constant, can lead to confusion with the association constant and it may be necessary to see the reaction or the equilibrium expression to know which is meant.)
, used for the acid dissociation constant, can lead to confusion with the association constant and it may be necessary to see the reaction or the equilibrium expression to know which is meant.)
Acid dissociation constants are sometimes expressed by p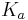 , which is defined as:
, which is defined as:
This p notation is seen in other contexts as well; it is mainly used for covalent dissociations (i.e., reactions in which chemical bonds are made or broken) since such dissociation constants can vary greatly.
notation is seen in other contexts as well; it is mainly used for covalent dissociations (i.e., reactions in which chemical bonds are made or broken) since such dissociation constants can vary greatly.
A molecule can have several acid dissociation constants. In this regard, that is depending on the number of the protons they can give up, we define monoprotic, diprotic and triprotic acids. The first (e.g. acetic acid or ammonium) have only one dissociable group, the second (carbonic acid, bicarbonate, glycine) have two dissociable groups and the third (e.g. phosphoric acid) have three dissociable groups. In the case of multiple pK values they are designated by indices: pK1, pK2, pK3 and so on. For amino acids, the pK1 constant refers to its carboxyl (-COOH) group, pK2 refers to its amino (-NH3) group and the pK3 is the pK value of its side chain.
![H_3 B \rightleftharpoons\ H ^ %2B %2B H_2 B ^ - \qquad K_1 = {[H ^ %2B] \cdot [H_2 B ^ -] \over [H_3 B]} \qquad pK_1 = - \log K_1](/2012-wikipedia_en_all_nopic_01_2012/I/980590c88a8f9b714ea1cd9a07dc4a09.png)
![H_2 B ^ - \rightleftharpoons\ H ^ %2B %2B H B ^ {-2} \qquad K_2 = {[H ^ %2B] \cdot [H B ^{-2}] \over [H_2 B^ -]} \qquad pK_2 = - \log K_2](/2012-wikipedia_en_all_nopic_01_2012/I/cab90daeb7bd0ac31fda75688302766b.png)
![H B ^{-2} \rightleftharpoons\ H ^ %2B %2B B ^{-3} \qquad K_3 = {[H ^ %2B] \cdot [ B ^ {-3}] \over [H B ^ {-2}]} \qquad pK_3 = - \log K_3](/2012-wikipedia_en_all_nopic_01_2012/I/1fb1239e8d1d56b9b3c4e629fec9050e.png)
Dissociation constant of water
As a frequently used special case, the dissociation constant of water is often expressed as Kw:
![K_w = [\mbox{H}^%2B] [\mbox{OH}^-]](/2012-wikipedia_en_all_nopic_01_2012/I/4b9e2e252a7d53f8b0da6859787cec32.png)
The concentration of water ![\left[ \mbox{H}_2\mbox{O} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/0790e5e6b5eab215ab1c4bcfe59ba835.png) is not included in the definition of Kw, for reasons described in the article equilibrium constant.
is not included in the definition of Kw, for reasons described in the article equilibrium constant.
The value of Kw varies with temperature, as shown in the table below. This variation must be taken into account when making precise measurements of quantities such as pH.
| Water temperature | Kw / 10−14 | pKw |
|---|---|---|
| 0°C | 0.1 | 14.92 |
| 10°C | 0.3 | 14.52 |
| 18°C | 0.7 | 14.16 |
| 25°C | 1.2 | 13.92 |
| 30°C | 1.8 | 13.75 |
| 50°C | 8.0 | 13.10 |
| 60°C | 12.6 | 12.90 |
| 70°C | 21.2 | 12.67 |
| 80°C | 35 | 12.46 |
| 90°C | 53 | 12.28 |
| 100°C | 73 | 12.14 |
See also
References
- ^ Zhou, H.; Rivas, G.; Minton, A. (2008). "Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences". Annual review of biophysics 37: 375–397. doi:10.1146/annurev.biophys.37.032807.125817. PMC 2826134. PMID 18573087. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2826134.
- ^ Minton, A. P. (2001). "The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media". The Journal of biological chemistry 276 (14): 10577–10580. doi:10.1074/jbc.R100005200. PMID 11279227.
- ^ Livnah, O.; Bayer, E.; Wilchek, M.; Sussman, J. (1993). "Three-dimensional structures of avidin and the avidin-biotin complex". Proceedings of the National Academy of Sciences of the United States of America 90 (11): 5076–5080. Bibcode 1993PNAS...90.5076L. doi:10.1073/pnas.90.11.5076. PMC 46657. PMID 8506353. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=46657.
- ^ Johnson, R.; Mccoy, J.; Bingman, C.; Phillips Gn, J.; Raines, R. (2007). "Inhibition of human pancreatic ribonuclease by the human ribonuclease inhibitor protein". Journal of molecular biology 368 (2): 434–449. doi:10.1016/j.jmb.2007.02.005. PMC 1993901. PMID 17350650. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1993901.
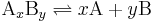
![K_{d} = \frac{[A]^x \times [B]^y}{[A_x B_y]}](/2012-wikipedia_en_all_nopic_01_2012/I/fa734f7c67752b156fc481a917e07f30.png)
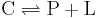
![K_{d} = \frac{\left[ \mathrm{P} \right] \left[ \mathrm{L} \right]}{\left[ \mathrm{C} \right]}](/2012-wikipedia_en_all_nopic_01_2012/I/02d9662e84613b8f2ab83ae3d30de36c.png)
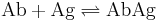
![K_{a} = \frac{\left[ \text{AbAg} \right]}{\left[ \text{Ab} \right] \left[ \text{Ag} \right]} = \frac{1}{K_{d}}](/2012-wikipedia_en_all_nopic_01_2012/I/d0af9d86400d19d67b24c34cb1a1c325.png)